приведение матрицы к ступенчатому виду методом Гаусса

В качестве примера работы с матрицами рассмотрим алгоритм Гаусса приведения матрицы к ступенчатому виду. Метод Гаусса - один из основных результатов линейной алгебры и аналитической геометрии, к нему сводятся множество других теорем и методов линейной алгебры (теория и вычисление определителей, решение систем линейных уравнений, вычисление ранга матрицы и обратной матрицы, теория базисов конечномерных векторных пространств и т.д.).

Напомним, что матрица A с элементами aij

называется ступенчатой, если она обладает следующими двумя свойствами:

если в матрице есть нулевая строка, то все строки ниже нее также нулевые;
пусть aij

не равное 0 -- первый ненулевой элемент в строке с индексом i, т.е. элементы ail = 0 при l < j. Тогда все элементы в j-м столбце ниже элемента aij

равны нулю, и все элементы левее и ниже aij

также равны нулю: akl = 0 при k > i и l =< j.

Ступенчатая матрица выглядит примерно так:

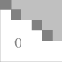
здесь тёмными квадратиками отмечены первые ненулевые элементы строк матрицы. Белым цветом изображаются нулевые элементы, серым цветом - произвольные элементы.

Алгоритм Гаусса использует элементарные преобразования матрицы двух типов.

Преобразование первого рода: две строки матрицы меняются местами, и при этом знаки всех элементов одной из строк изменяются на противоположные.
Преобразование второго рода: к одной строке матрицы прибавляется другая строка, умноженная на произвольное число.

Элементарные преобразования сохраняют определитель и ранг матрицы, а также множество решений линейной системы. Алгоритм Гаусса приводит произвольную матрицу элементарными преобразованиями к ступенчатому виду. Для ступенчатой квадратной матрицы определитель равен произведению диагональных элементов, а ранг - числу ненулевых строк (рангом по определению называется размерность линейной оболочки строк матрицы).

Метод Гаусса в математическом варианте состоит в следующем:

ищем сначала ненулевой элемент в первом столбце. Если все элементы первого столбца нулевые, то переходим ко второму столбцу, и так далее.
Если нашли ненулевой элемент в k- й строке, то при помощи элементарного преобразования первого рода меняем местами первую и k-ю строки, добиваясь того, чтобы первый элемент первой строки был отличен от нуля;
используя элементарные преобразования второго рода, обнуляем все элементы первого столбца, начиная со второго элемента. Для этого от строки с номером k вычитаем первую строку, умноженную на коэффициент ak1/a11
.
переходим ко второму столбцу (или j-му, если все элементы первого столбца были нулевыми), и в дальнейшем рассматриваем только часть матрицы, начиная со второй строки и ниже. Снова повторяем пункты 1) и 2) до тех пор, пока не приведем матрицу к ступенчатому виду.

Программистский вариант метода Гаусса имеет три отличия от математического:

индексы строк и столбцов матрицы начинаются с нуля, а не с единицы;
недостаточно найти просто ненулевой элемент в столбце. В программировании все действия с вещественными числами производятся приближенно, поэтому можно считать, что точного равенства вещественных чисел вообще не бывает. Некоторые компиляторы даже выдают предупреждения на каждую операцию проверки равенства вещественных чисел. Поэтому вместо проверки на равенство нулю числа aij

следует сравнивать его абсолютную величину ?aij? с очень маленьким числом ? (например, ? = 0.00000001). Если ?aij? =< ?, то следует считать элемент aij
нулевым;
при обнулении элементов j-го столбца, начиная со строки i + 1, мы к k-й строке, где k > i, прибавляем i-ю строку, умноженную на коэффициент r = -akj/aij
:

r = -akj/aij. ak = ak + r * ai
Такая схема работает нормально только тогда, когда коэффициент r по абсолютной величине не превосходит единицы. В противном случае, ошибки округления умножаются на большой коэффициент и, таким образом, экспоненциально растут. Математики называют это явление неустойчивостью вычислительной схемы. Если вычислительная схема неустойчива, то полученные с ее помощью результаты не имеют никакого отношения к исходной задаче. В нашем случае схема устойчива, когда коэффициент r = -akj/aij

не превосходит по модулю единицы. Для этого должно выполняться неравенство
?aij? >= ?akj? при k > i
Отсюда следует, что при поиске разрешающего элемента в j-м столбце необходимо найти не первый попавшийся ненулевой элемент, а максимальный по абсолютной величине. Если он по модулю не превосходит ?, то считаем, что все элементы столбца нулевые; иначе меняем местами строки, ставя его на вершину столбца, и затем обнуляем столбец элементарными преобразованиями второго рода.
Ниже дан полный текст программы на Си, приводящей вещественную матрицу к ступенчатому виду. Функция, реализующая метод Гаусса, одновременно подсчитывает и ранг матрицы. Программа вводит размеры матрицы и ее элементы с клавиатуры и вызывает функцию приведения к ступенчатому виду. Затем программа печатает ступенчатый вид матрицы и ее ранг. В случае квадратной матрицы также вычисляется и печатается определитель матрицы, равный произведению диагональных элементов ступенчатой матрицы.
При реализации метода Гаусса используется схема построения цикла с помощью инварианта, см. раздел 1.5.2. В цикле меняются две переменные -- индекс строки i, 0 =< i < m - 1, и индекс столбца j, 0 =< j < n - 1. Инвариантом цикла является утверждение о том, что часть матрицы (математики говорят минор) в столбцах 0,1,...j - 1 приведена к ступенчатому виду и что первый ненулевой элемент в строке i - 1 стоит в столбце с индексом меньшим j. В теле цикла рассматривается только минор матрицы в строках i,...,m - 1 и столбцах j,...,n - 1. Сначала ищется максимальный по модулю элемент в j-м столбце. Если он по абсолютной величине не превосходит ?, то j увеличивается на единицу (считается, что столбец нулевой). Иначе перестановкой строк разрешающий элемент ставится на вершину j-го столбца минора, и затем столбец обнуляется элементарными преобразованиями второго рода. После этого оба индекса i и j увеличиваются на единицу. Алгоритм завершается, когда либо i = m, либо j = n. По окончании алгоритма значение переменной i равно числу ненулевых строк ступенчатой матрицы, т.е.

рангу исходной матрицы.
Для вычисления абсолютной величины вещественного числа x типа double мы пользуемся стандарной математической функцией fabs(x), описанной в стандартном заголовочном файле "math.h.
#include <stdio.h> // Описания функций ввода-вывода #include <math.h> // Описания математических функций #include <stdlib.h> // Описания функций malloc и free
// Прототип функции приведения матрицы // к ступенчатому виду. // Функция возвращает ранг матрицы int gaussMethod( int m, // Число строк матрицы int n, // Число столбцов матрицы double *a, // Адрес массива элементов матрицы double eps // Точность вычислений );
int main() { int m, n, i, j, rank; double *a; double eps, det;
printf("Введите размеры матрицы m, n: "); scanf("%d%d", &m, &n);
// Захватываем память под элементы матрицы a = (double *) malloc(m * n * sizeof(double));
printf("Введите элементы матрицы:\n"); for (i = 0; i < m; ++i) { for (j = 0; j < n; ++j) { // Вводим элемент с индексами i, j scanf("%lf", &(a[i*n + j])); } }
printf("Введите точность вычислений eps: "); scanf("%lf", &eps);
// Вызываем метод Гаусса rank = gaussMethod(m, n, a, eps);
// Печатаем ступенчатую матрицу printf("Ступенчатый вид матрицы:\n"); for (i = 0; i < m; ++i) { // Печатаем i-ю строку матрицы for (j = 0; j < n; ++j) { printf( // Формат %10.3lf означает 10 "%10.3lf ", // позиций на печать числа, a[i*n + j] // 3 знака после точки ); } printf("\n"); // Перевести строку }
// Печатаем ранг матрицы printf("Ранг матрицы = %d\n", rank);
if (m == n) { // Для квадратной матрицы вычисляем и печатаем // ее определитель det = 1.0; for (i = 0; i < m; ++i) { det *= a[i*n + i]; } printf("Определитель матрицы = %.3lf\n", det); }
free(a); // Освобождаем память return 0; // Успешное завершение программы }
// Приведение вещественной матрицы // к ступенчатому виду методом Гаусса с выбором // максимального разрешающего элемента в столбце. // Функция возвращает ранг матрицы int gaussMethod( int m, // Число строк матрицы int n, // Число столбцов матрицы double *a, // Адрес массива элементов матрицы double eps // Точность вычислений ) { int i, j, k, l; double r;

i = 0; j = 0; while (i < m && j < n) { // Инвариант: минор матрицы в столбцах 0..j-1 // уже приведен к ступенчатому виду, и строка // с индексом i-1 содержит ненулевой эл-т // в столбце с номером, меньшим чем j
// Ищем максимальный элемент в j-м столбце, // начиная с i-й строки r = 0.0; for (k = i; k < m; ++k) { if (fabs(a[k*n + j]) > r) { l = k; // Запомним номер строки r = fabs(a[k*n + j]); // и макс. эл-т } } if (r <= eps) { // Все элементы j-го столбца по абсолютной // величине не превосходят eps. // Обнулим столбец, начиная с i-й строки for (k = i; k < m; ++k) { a[k*n + j] = 0.0; } ++j; // Увеличим индекс столбца continue; // Переходим к следующей итерации }
if (l != i) { // Меняем местами i-ю и l-ю строки for (k = j; k < n; ++k) { r = a[i*n + k]; a[i*n + k] = a[l*n + k]; a[l*n + k] = (-r); // Меняем знак строки } }
// Утверждение: fabs(a[i*n + k]) > eps
// Обнуляем j- й столбец, начиная со строки i+1, // применяя элем. преобразования второго рода for (k = i+1; k < m; ++k) { r = (-a[k*n + j] / a[i*n + j]);
// К k-й строке прибавляем i-ю, умноженную на r a[k*n + j] = 0.0; for (l = j+1; l < n; ++l) { a[k*n + l] += r * a[i*n + l]; } }
++i; ++j; // Переходим к следующему минору }
return i; // Возвращаем число ненулевых строк }
Приведем два примера работы этой программы. В первом случае вводится вырожденная матрица размера 4 ? 4:
Введите размеры матрицы m, n: 4 4 Введите элементы матрицы: 1 2 3 4 4 3 2 1 5 6 7 8 8 7 6 5 Введите точность вычислений eps: 0.00001 Ступенчатый вид матрицы: 8.000 7.000 6.000 5.000 0.000 1.625 3.250 4.875 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 Ранг матрицы = 2 Определитель матрицы = 0.000
Во втором случае вводится матрица размера 3 ? 4 максимального ранга:
Введите размеры матрицы m, n: 3 4 Введите элементы матрицы: 1 0 2 1 2 1 0 -1 1 0 1 0 Введите точность вычислений eps: 0.00001 Ступенчатый вид матрицы: 2.000 1.000 0.000 -1.000 0.000 0.500 -2.000 -1.500 0.000 0.000 -1.000 -1.000 Ранг матрицы = 3

Содержание раздела