Особенности применения косинуса как функции меры угла

О величине угла в n-мерном пространстве мы можем судить только по его косинусу. Однако косинус не является монотонной функцией и в общем случае может служить мерой угла, если диапазон изменения этого угла не превышает

.

Составим по (6.11) симметричную матрицу S, включенную в табл. 6.1

косинусов углов между всеми нормалями к граням верхней (нижней) поверхности выпуклого многогранника R.

Таблица 6.1.

ГраньНормальN1 N2... Nr+n

p1	N1	1	cos(N1,N2)	...	cos(N1,Nr+n)
p2	N2	cos (N2,N1)	1	...	cos(N2,Nr+n)
...	...	...	...	...	...
pr	Nr	cos(Nr,N1)	cos(Nr,N2)	...	cos(Nr,Nr+n)
pr+1	Nr+1	cos(Nr+1,N1)	cos(Nr+1,N2)	...	cos(Nr+1,Nr+n)
...	...	...	...	...	...
pr+n	Nr+n	cos(Nr+n, N1)	cos(Nr+n,N2)	...	1

Выберем строку, соответствующую некоторой грани. Для комплектации граней, совместно с выбранной образующих общую вершину, выделим в этой строке n минимальных отличных от 0 и

углов, то есть n максимальных косинусов, отличных от 1 и -1. Тем самым мы отдаем предпочтение вершинам с наиболее "пологими" склонами. При корректно сформулированной задаче такие грани "вокруг" некоторых вершин должны найтись. При этом углы между нормалями к граням, образующим общую вершину, не превышают . Следовательно, косинус может служить функцией меры углов в диапазоне их изменения.

Поясним выбор последовательности n косинусов.

Выбранная грань может быть параллельна некоторой другой грани или координатной плоскости, т.е. угол между их нормалями может быть равен либо нулю, либо

. Очевидно, такие грани не могут быть образующими одной вершины.

На рис. 6.6 Qнижн={p1, p2, p3, p4}.

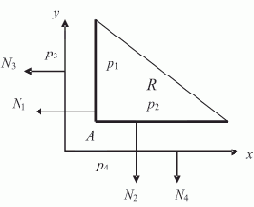
Рис. 6.6.  Пример, показывающий, когда грани не могут быть образующими одной вершины

Таблица косинусов углов имеет вид

Таблица 6.2.

ГраньНормальN1 N2N3 N4

p1	N1	1	0	1	0
p2	N2	0	1	0	1
p3	N3	1	0	1	0
p4	N4	0	1		0

Из первой строки, допуская лишь одну единицу cos(N1,N1)=1), находим возможные образующие {p1, p2}. При этом поиск элементов последовательности ведем слева направо. Проверка подтверждает правильность выбора вершины A.
Аналогично, из второй строки находим {p2, p1}, что определяет ту же вершину. Третья строка определяет возможное множество образующих {p3, p2}, что не подтверждается проверкой. Четвертая строка также не определяет правильный выбор образующих {p4, p1}.

Обратим внимание на то, что все вышесказанные предположения и теоремы касаются граней, о которых доподлинно известно, что они входят в состав поверхности многогранника допустимых решений. Важным источником неприятностей являются координатные плоскости. Ведь мы не знаем, являются ли они действительными гранями, и вынуждены относить их к возможным. Отсюда и возможная ошибочность выводов.

На рис. 6.7 Qнижн={p1, p2, p3, p4, p5}.

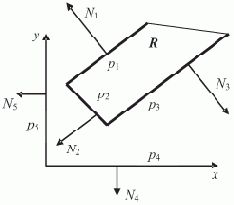
Рис. 6.7.  "Критические" случаи

Таблица косинусов углов имеет вид

Таблица 6.3. ГраньНормальN1 N2N3 N4 N5

p1	N1	1	0	-1	-v2/2	v2/2
p2	N2	0	1	0	v2/2	v2/2
p3	N3	-1	0	1	v2/2	-v2/2
p4	N4	-v2/2	v2/2	v2/2	1	0
p5	N5	v2/2	v2/2	-v2/2	0	1

Легко видеть, что анализ любой строки не позволит обнаружить вершину многогранника R.

Действительно, по первой строке формируется предполагаемое множество образующих {p1, p4}. Однако пересечение этих прямых не дает искомую вершину. И так — по всем строкам. Если бы было установлено, что ось y не входит в состав поверхности R, то соответствующий косинус можно бы было игнорировать, что привело бы к правильному выбору множества образующих {p1, p2}.

Анализ этого примера наводит на мысль: обязательно ли формировать верхнюю (нижнюю) поверхность до конца, присоединяя координатные плоскости? Ведь количество действительных граней, составляющих ее, достаточно для осуществления поиска вершины. А именно, если в выражении (6.7) r n, то на первом этапе поиска исключим из рассмотрения координатные плоскости. Это приведет к исключению из табл. 6.3

двух последних строк и столбцов. Легко видеть, что поиск вершины осуществляется успешно.

На рис. 6.8 демонстрируется случай, когда, несмотря на выполнение указанного выше неравенства, к поиску вершины необходимо подключать координатные плоскости.




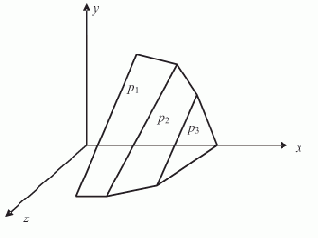
Рис. 6.8.  Необходимость анализа координатных плоскостей

Три плоскости p1, p2, p3 совместно не являются образующими одной вершины. Только включение в рассмотрение плоскостей z = 0 или y = 0 позволяет найти вершины многогранника допустимых решений.

Грань может иметь нормаль, угол которой с нормалями некоторых "далеких" граней превышает . Например, углы между нормалями к координатным плоскостям составляют . Здесь использование косинуса может привести к неоднозначности при упорядочении углов.

Тогда воспользуемся следующим предположением:

На верхней (нижней) поверхности выпуклого многогранника R существует грань, нормаль к которой составляет с нормалями ко всем другим граням этой поверхности углы, не превышающие .

Это — предположение об обязательном существовании некоторых "срединных" граней, нормали к которым близки к середине диапазона изменения таких нормалей, — диапазона .

На рис. 6.9 отражена попытка представления некоторых крайних случаев, иллюстрирующих на плоскости существование "срединных" граней для разных выпуклых многогранников.


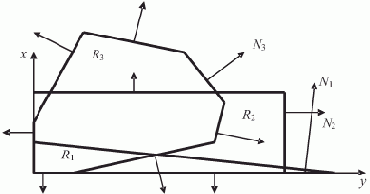
Рис. 6.9.  К существованию углов, не превышающих pi

Так, в многограннике R1 (треугольник) угол между нормалью N1

и другими нормалями не превышает . В прямоугольнике R2

максимальный угол, например, между нормалью N2 и другими нормалями, составляет . В многоугольнике R3, к примеру, нормаль N3

составляет со всеми нормалями угол, меньше .

Таким образом, мы предположили существование хотя бы одной грани, при анализе которой с помощью косинусов удается избежать искажений в определении того, в каком отношении находятся углы, которые нормаль к этой грани образует с нормалями к другим граням поверхности. Исключается случай, когда большему углу соответствует и больший косинус. Это приводит к необходимости одновременного параллельного анализа многих граней поверхности в качестве начальных, так как успех может быть достигнут не всегда.


Содержание раздела

---

---

Главная сайта

---