Параллельное решение "плоской" задачи НП
Постановка задачи:
f(x,y)

при ограничениях
g1(x,y)

... gm(x,y)

Могут быть условия x,y

Предположим:
- Все ограничения разрешимы относительно всех переменных.
- Ограничения и, возможно, условия неотрицательности решения образуют область R, ограниченную со всех сторон (рис. 6.2).
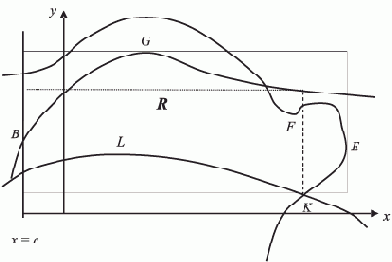
Рис. 6.2. "Плоская" нелинейная задача оптимизации с нелинейными ограничениями
Предположим, как на рисунке, m = 4. (Одно ограничение, x-c

Решая попарно все равенства (границы R), полученные по ограничениям, и проверяя точки пересечения на удовлетворение остальным неравенствам-ограничениям, найдём все вершины, в нашем примере — {A, B, C, K}.
Координаты найденных вершин дают начальную информацию (прямоугольник показан пунктиром) о "минимальном" прямоугольнике D, включающем в себя область R. Однако некоторые кривые, ограничивающие R, сопряженные с двумя вершинами, могут, имея экстремум по некоторым координатам между ними, "выходить" из этого прямоугольника. Точки такого выхода надо найти, проверить на принадлежность R, если они существуют, и расширить D.
Для каждого i = 1, ... , m, разрешим gi
относительно x. Получим (возможно, неоднозначную) функцию
x =

Найдем множество экстремумов этой функции, решив уравнение
x' =

Для каждой точки экстремума проверяем, принадлежит ли она области R, т.е. выполняются ли для нее все ограничения. Такой точкой на рисунке является точка E.
Теперь то же самое надо проделать, разрешив все функции gi
относительно y,
y = ? i (x)
Найдем множество экстремумов этой функции, удовлетворяющих всем ограничениям. На рисунке это точки G, F, M, L.
Теперь мы нашли все точки, которые помогут нам очертить прямоугольник D, полностью вмещающий область R — область возможных решений задачи. Границы этого прямоугольника определяются минимальными и максимальными значениями координат всех найденных точек — точек пересечения кривых ограничений и точек экстремумов этих кривых, удовлетворяющих всем ограничениям задачи.
В нашем примере пусть A = (xA, yA), B = (xB, yB) и т.д. Тогда
xD1 = min{xA, xB, xG, xC, xF, xE, xM, xK, xL } = xA = xB,
xD2 = max{xA, xB, xG, xC, xF, xE, xM, xK, xL} = xE ,
yD1 = min{yA, yB, yG, yC, yF, yM, yE, yK, yL} = yK,
yD2 = max{yA, yB, yG, yC, yF, yM, yE, yK, yL} = yG.
Воспользуемся методом "сеток". Покроем область D сеткой с шагом ? x по x и ? y по y. Испытывая каждый узел на принадлежность R, и находя в нем значение f(x, y), выберем максимальное.
Допускается обобщение метода решения для произвольной размерности.
