Граф-схемы параллельных алгоритмов
Представим себе программу решения задачи, которая отображает последовательное изложение алгоритма на машинном языке, ассемблере или ЯВУ. Предположим, что, анализируя эту программу, нам удалось разбить её на отдельные модули и выделить для каждого из них множества входных и выходных данных так, чтобы установить взаимодействие модулей по информации.
Например, программа F представляется как
F = F1(X1 , X2 ; X3 , X4 ) F2 (X2 ; X5 ) F3 (X3 ; X6 ) F4 (X1 , X4 ; X7 ) F5 (X3 , X4 , X5 ; X8 ) F6 (X3 , X4 , X7 ; X9 ) F7 (X5 , X7 ; X10) F8 (X6 , X8 , X9 , X10 ; Y), где точкой с запятой отделены входные данные от выходных, X = {X1, X2} — исходные данные задачи, Y — выходные данные или результат.
Итак, мы разбили заданный алгоритм решения задачи на ряд модулей, операторов, работ и установили информационную взаимосвязь этих работ. Чтобы подчеркнуть общность задач и методов распараллеливания, не ограничивающуюся применением только для ВС, будем пользоваться термином работа.
Для решения задач оптимального выполнения работ многими исполнителями (т.е. процессорами ВС) нам понадобятся временные оценки выполнения как программы в целом, так и каждого выделенного модуля, т.е. каждой работы. Эти оценки могут быть выполнены как экспериментально, так и на основе количества операций и производительности процессоров, предполагаемых к использованию.
Пусть относительно данного алгоритма и предполагаемой ВС нам известны следующие оценки T = {t1, t2, ... , t8}.
Тогда, чтобы отразить прохождение обрабатываемой информации и выявить возможности распараллеливания, представим информационную граф-схему алгоритма или информационный граф G (рис. 7.1). Вершины соответствуют работам. Дуги отражают частичную упорядоченность работ.
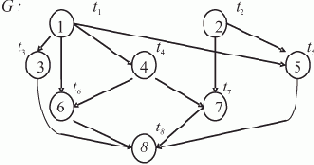
Рис. 7.1. Информационный граф алгоритма
А именно, если работа ? использует в качестве входной информации результат выполнения работы


Граф G — взвешенный, ориентированный и не содержит контуров. (Т.к. время выполнения алгоритма конечно, то программные циклы либо погружены внутрь работ, либо развёрнуты.)
Например, представим себе информационный граф, соответствующий скалярному умножению векторов заданной длины: A = B ? C способом "пирамиды", В = {b1 , ... , b8}, C = {c1 , ... , c8}. Схема счёта показана на рис. 7.2.
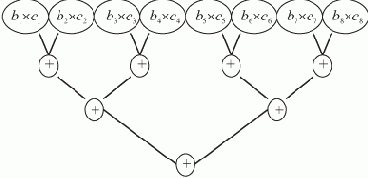
Рис. 7.2. Схема счёта "пирамидой"
Примем время сложения равным единице. Время умножения пусть превышает время сложения в четыре раза. Информационный граф G, соответствующий счёту способом "пирамиды", представлен на рис. 7.3.
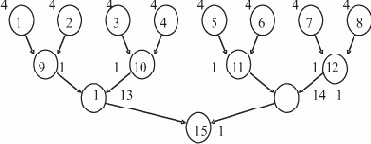
Рис. 7.3. Информационный граф — "пирамида"
Мы рассмотрели составление информационных графов. Можно рассматривать информационно-логические графы, если учитывать альтернативные ветви алгоритмов.
Например, может быть целесообразным следующее разбиение программы (алгоритма) на модули (работы):
F = F1(X1; X2) if A then F2(X2; X3) else F3(X1;X4) F4(X1, X3, X4; Y).
Информационно-логический граф G — на рис. 7.4.
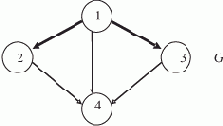
Рис. 7.4. Информационно-логический граф
Преемственность информации (1


Рассмотрение информационно-логических графов сильно усложняет решение задач оптимизации параллельных вычислений. Практически ограничиваются планированием выполнения самой сложной, трудоемкой ветви алгоритма или решают её для разных ветвей отдельно, — т.е. сводят оптимизацию к рассмотрению только информационных графов.
Для формальных исследований информационный граф G представляется матрицей следования S, или, с добавлением столбцов весов, — расширенной матрицей следования S*. При этом, т.к. граф G не содержит контуров (циклов), то S может быть сведена к треугольной "правильным" выбором нумерации вершин. Ниже (рис. 7.5) приведены матрицы S и S* для графа, представленного на рис. 7.1, и для некоторых известных значений весов.
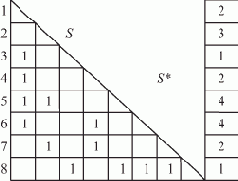
Рис. 7.5. Матрица следования с задающими связями
Определение 1. Назовём все связи по информации, обусловленные исходным видом графа G, задающими связями.
Определение 2.
Путями в графе G будем называть последовательности вершин вида a1, a2 , ... , as такие, что для любой пары соседних вершин ai и ai+1 существует дуга, исходящая из вершины ai и входящая в вершину ai+1.
Будем считать все пути в графе G допустимыми, т.е. реально существующими ветвями отображаемой программы.
Определение 3. Длиной пути в информационном графе G назовём сумму весов вершин, составляющих этот путь.
Определение 4. Путь максимальной длины Tкр в информационном графе G назовём критическим.
В одном графе может быть несколько путей равной длины, являющихся критическими.
Если в графе G есть дуга, исходящая из вершины a и входящая в вершину b, т.е. существует задающая связь a




Определение 5. Множество связей, которые введены направленно внутри всех пар работ, принадлежащих одному пути в графе G и не связанных задающими связями, назовём множеством транзитивных связей.
Транзитивные связи полностью определяются задающими связями.
Алгоритм 1 дополнения треугольной матрицы S транзитивными связями.
- Организуем просмотр сверху вниз строк матрицы следования S.
- В очередной i-й строке организуем просмотр элементов в порядке увеличения j номеров столбцов.
- Если (i, j)=1, складываем строки i и j по операции дизъюнкции.
- Если исходная матрица следования S нетреугольная, последовательный просмотр её строк производится неоднократно до установления факта неизменности окончательно полученной матрицы.)
Конец алгоритма.
В представленном выше примере после введения всех транзитивных связей матрица следования S примет вид, представленный на рисунке 7.6)рисунке 7.6 (введённые транзитивные связи выделены курсивом).
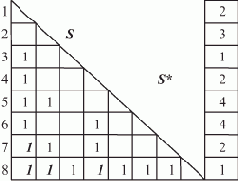
Рис. 7.6. Матрица следования с транзитивными связями
С помощью введения транзитивных связей в нетреугольной матрице следования устанавливается наличие контуров в графе G. О наличии контуров свидетельствуют появившиеся ненулевые диагональные элементы, указывающие на связь вида a

Например, пусть задан граф G на рис. 7.7.
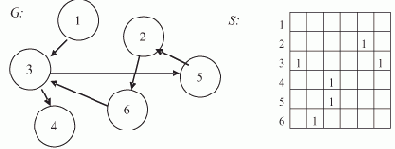
Рис. 7.7. Граф алгоритма и матрица следования
После первого шага преобразования S принимает вид, показанный на рис. 7.8.
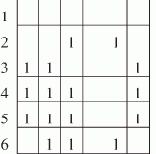
Рис. 7.8. Первый шаг обнаружения контура
После второго шага преобразования S принимает вид, показанный на рис. 7.9.
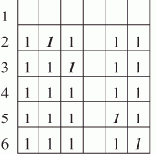
Рис. 7.9. Обнаружение контура
Т.к. на главной диагонали матрицы появились единицы, то граф G содержит циклы (контуры). Из рисунка графа виден цикл 2




Определение 6. Работы a и b будем называть взаимно независимыми, если в матрице следования S выполняется условие (a, b) = (b, a) = 0.
Определение 7. Работы {ai}, i = 1, ... , s, образуют полное множество взаимно независимых работ (ПМВНР), если для любой работы j


Например, для графа G, представленного на рис. 7.1, после введения транзитивных связей, что учтено в матрице следования на рис. 7.6, можно установить следующие ПМВНР: {1,2}, {2,3,4}, {3,4,5}, {2,3,6}, {3,5,6,7}, {8}.
